写在博客之前

算法初步

Adaline可以看作是对感知器算法的优化和改进，Adaline算法定义了最小化连续性代价函数的概念，这为理解如逻辑回归、支持向量机和回归模型等更高级的机器学习算法奠定了基础。

定义代价函数：
$$
J(w) = \frac{1}{2}\sum_{i=1}^{m}(y^{(i)}-h_w(x^{(i)}))^2
\\ h_w(x) = w^Tx
$$
我们要优化目标函数$h_w(x)$，使得输出值符合实际值，就要尽可能降低代价函数$J(w)$,找到使得代价函数最小的w。

利用梯度下降求最优解：
$$
w_j:=w_j-\Delta w_j \
\Delta w_j = \eta \frac{\delta J}{\delta w_j}=\eta \sum_{i=1}^{m}(h_w(x^{(i)})-y^{(i)})x_j^{(i)}
$$

代码实现

定义类AdalineGD封装分类算法，调用fit方法拟合数据，训练模型；调用predict方法测试模型，返回分类类标（1，-1）。

定义plot_decision_regions类，将分类结果可视化。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap

class AdalineGD(object):
    def __init__(self, eta=0.01, n_iter=50, random_state=1):        
        self.eta = eta        
        self.n_iter = n_iter        
        self.random_state = random_state

    def fit(self, X, y):
        rgen = np.random.RandomState(self.random_state)        
        self.w_ = rgen.normal(loc=0.0, scale=0.01,size=1 + X.shape[1])        
        self.cost_ = []
        for i in range(self.n_iter):            
            net_input = self.net_input(X)            
            output = self.activation(net_input)            
            errors = (y - output)            
            self.w_[1:] += self.eta * X.T.dot(errors)            
            self.w_[0] += self.eta * errors.sum()            
            cost = (errors**2).sum() / 2.0            
            self.cost_.append(cost)        
        return self

    def net_input(self, X):        
        """Calculate net input"""        
        return np.dot(X, self.w_[1:]) + self.w_[0]

    def activation(self,X):
        return X

    def predict(self, X):        
        """Return class label after unit step"""        
        return np.where(self.activation(self.net_input(X)) >= 0.0, 1, -1)

def plot_decision_regions(X, y, classifier, resolution=0.02):

    # setup marker generator and color map    
    markers = ('s', 'x', 'o', '^', 'v')    
    colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')    
    cmap = ListedColormap(colors[:len(np.unique(y))])

    # plot the decision surface    
    x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1    
    x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1    
    xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),                           
                           np.arange(x2_min, x2_max, resolution))    
    Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)    
    Z = Z.reshape(xx1.shape)    
    plt.contourf(xx1, xx2, Z, alpha=0.3, cmap=cmap)    
    plt.xlim(xx1.min(), xx1.max())    
    plt.ylim(xx2.min(), xx2.max())

    # plot class samples    
    for idx, cl in enumerate(np.unique(y)):        
        plt.scatter(x=X[y == cl, 0],                    
                    y=X[y == cl, 1],                    
                    alpha=0.8,                    
                    c=colors[idx],                    
                    marker=markers[idx],                    
                    label=cl,                    
                    edgecolor='black')

测试选用不同学习率0.01和0.001，可以从下图看到，选用学习率0.01使得代价函数随着迭代次数的增加而增加，而选用学习率0.001使得代价函数逐渐收敛。在实际解决问题的过程中，选择过大的学习率可能会错过全局最优解，我们应该选择合适的学习率。

df = pd.read_csv('https://archive.ics.uci.edu/ml/' 
...              'machine-learning-databases/iris/iris.data', 
...               header=None)
# select setosa and versicolor 
y = df.iloc[0:100, 4].values 
y = np.where(y == 'Iris-setosa', -1, 1)

# extract sepal length and petal length 
X = df.iloc[0:100, [0, 2]].values

fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(10, 4))
ada1 = AdalineGD(n_iter=10, eta=0.01).fit(X, y)
ax[0].plot(range(1, len(ada1.cost_) + 1),np.log10(ada1.cost_), marker='o')
ax[0].set_xlabel('Epochs')
ax[0].set_ylabel('log(Sum-squared-error)')
ax[0].set_title('Adaline - Learning rate 0.01')
ada2 = AdalineGD(n_iter=10, eta=0.0001).fit(X, y)
ax[1].plot(range(1, len(ada2.cost_) + 1),ada2.cost_, marker='o')
ax[1].set_xlabel('Epochs')
ax[1].set_ylabel('Sum-squared-error')
ax[1].set_title('Adaline - Learning rate 0.0001')
plt.show()

为了优化算法性能，可以对数据做特征缩放，采用以下规则对数据进行特征缩放：
$$
x_{j}:=\frac{x_j-u_j}{\delta_j}
$$
$x_j$为训练样本n中第j个特征的所有值的向量，$u_j$、$\delta_j$分别是样本中第j个特征的平均值和标准差。

X_std = np.copy(X)
X_std[:,0] = (X[:,0] - X[:,0].mean()) / X[:,0].std()
X_std[:,1] = (X[:,1] - X[:,1].mean()) / X[:,1].std()
ada = AdalineGD(n_iter=15, eta=0.01)
ada.fit(X_std, y)
plot_decision_regions(X_std, y, classifier=ada)
plt.title('Adaline - Gradient Descent') 
plt.xlabel('sepal length [standardized]')
plt.ylabel('petal length [standardized]')
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()
plt.plot(range(1, len(ada.cost_) + 1), ada.cost_, marker='o')
plt.xlabel('Epochs')
plt.ylabel('Sum-squared-error')
plt.show()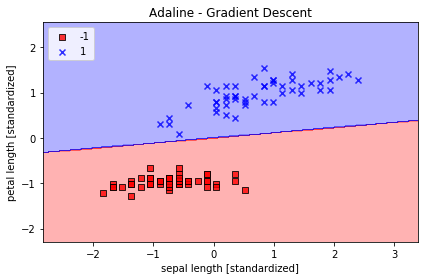

---

转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论，也可以邮件至 572108581@qq.com